Triangle xyz is equilateral with vertices located on circle w. – In the realm of geometry, triangle XYZ stands out as an equilateral gem, its vertices gracefully perched on the circumference of circle W. This intriguing configuration sparks a captivating exploration of geometric principles, where the interplay of sides, angles, and circles unfolds.
Triangle XYZ’s equilateral nature grants it unique properties, making it a subject of fascination in architecture, design, and beyond. As we delve into its characteristics and construction methods, we’ll unravel the secrets behind this harmonious geometric entity.
Triangle XYZ Equilateral Properties

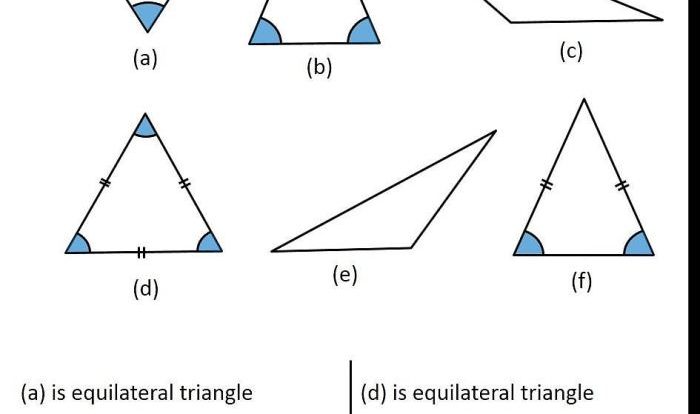
An equilateral triangle is a polygon with three equal sides and three equal angles. It is a regular polygon, meaning that all of its sides and angles are congruent. The angles of an equilateral triangle measure 60 degrees each, and the sum of the interior angles is 180 degrees.
Definition and Formula for Angles
The formula for calculating the angles of an equilateral triangle is:
∠A = ∠B = ∠C = 60°
where ∠A, ∠B, and ∠C represent the three angles of the triangle.
Relationship between Sides and Angles
In an equilateral triangle, the sides and angles are related by the following formula:
a = b = c = 2R sin(60°)
where a, b, and c represent the three sides of the triangle, and R is the radius of the circle that circumscribes the triangle.
Circle W and Triangle XYZ

Circle W is a circle that circumscribes triangle XYZ, meaning that all three vertices of the triangle lie on the circle. The center of circle W is equidistant from all three vertices of triangle XYZ.
Relationship between Circle W and Triangle XYZ
The relationship between circle W and triangle XYZ can be described as follows:
- The center of circle W is the circumcenter of triangle XYZ.
- The radius of circle W is equal to the length of the sides of triangle XYZ.
- The vertices of triangle XYZ divide circle W into three equal arcs.
Visual Representation
The following image shows triangle XYZ inscribed in circle W:
Geometric Constructions

Steps to Construct an Equilateral Triangle Inscribed in a Circle
- Draw a circle with center O and radius r.
- Choose a point A on the circle.
- Using a compass, construct an arc of radius r centered at A that intersects the circle at points B and C.
- Connect points A, B, and C to form triangle XYZ.
Geometric Principles Involved
The geometric principles involved in constructing an equilateral triangle inscribed in a circle include:
- The definition of an equilateral triangle
- The relationship between the center of a circle and its radius
- The properties of congruent arcs
Applications and Examples: Triangle Xyz Is Equilateral With Vertices Located On Circle W.

Examples of Real-World Applications
Equilateral triangles inscribed in circles are found in a variety of real-world applications, including:
- Architecture: The design of domes and arches
- Design: The creation of logos and symbols
- Engineering: The construction of bridges and other structures
Significance of Geometric Configuration, Triangle xyz is equilateral with vertices located on circle w.
The geometric configuration of an equilateral triangle inscribed in a circle is significant because it represents a balance of symmetry and stability. The equal sides and angles of the triangle create a sense of harmony, while the circle provides a sense of containment and unity.
Questions and Answers
What is the definition of an equilateral triangle?
An equilateral triangle is a triangle with all three sides of equal length.
How can you construct an equilateral triangle inscribed in a circle?
To construct an equilateral triangle inscribed in a circle, you can use a compass and straightedge to bisect the circle and then connect the points of intersection to form the vertices of the triangle.
What are some real-world applications of equilateral triangles inscribed in circles?
Equilateral triangles inscribed in circles are used in architecture, design, and engineering. For example, they can be found in the design of bridges, domes, and other structures.